Condiciones de equilibrio de un sólido
CONDICIONES DE EQUILIBRIO DE UN SÓLIDO
Frecuentemente necesitamos imponer el equilibrio de un sólido, o de parte de él.
Una propiedad clave del equilibrio estático es que el que cambie el punto de aplicación de las fuerzas no modifica el estado de equilibrio del sólido, siempre que las fuerzas se mantengan en su recta de acción original. Por eso el álgebra de vectores deslizantes es la herramienta básica a emplear cuando se trata de analizar el equilibrio de un cuerpo.
Las condiciones de equilibrio estático son pocas y sencillas. Se reducen a lo siguiente:
|
Hay equilibrio si el sistema de fuerzas que actúan es un sistema nulo. |
Es decir, el sistema de vectores deslizantes que representa a las fuerzas debe tener resultante y momento nulos.
La manera usual de imponer el equilibrio será: 1º, calcular la resultante y hacer que se anule (con lo que el campo de momentos será en todo caso uniforme). 2º, elegir un punto que resulte cómodo para calcular el momento respecto de él, y hacer que se anule también, con lo que hay garantías de que se anulará también en cualquier otro punto.
Con un conocimiento adecuado del álgebra de vectores deslizantes, lo anterior es en realidad todo lo que se necesita saber acerca del equilibrio de los cuerpos para abordar la asignatura.
CENTRO DE GRAVEDAD
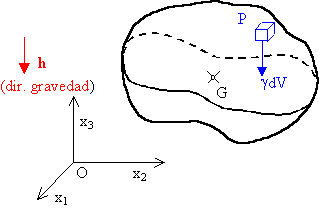
El peso de un cuerpo es el resultado de una distribución de fuerzas paralelas provocadas por la gravedad. Sobre cada diferencial de volumen del sólido, dV actúa una fuerza diferencial de módulo gdV, donde g es el peso específico en unidades de fuerza dividida por volumen (p.ej. N/m3). Si llamamos h al vector unitario en la dirección de la gravedad, la fuerza diferencial será hgdV.

Como se trata de un sistema de vectores paralelos, el momento mínimo es nulo, y el sistema admitirá reducción a su resultante aplicada en el eje central. Si G es un punto del eje central, debe cumplir la condición de que el momento sea nulo:
![]()
En donde h ha salido de la integral por ser un vector constante. Podríamos usar la ecuación anterior para encontrar un punto G del eje central, pero queremos plantear algo un poco más exigente: nos preguntamos si habrá un punto G tal que el eje central del sistema de fuerzas pase por él para cualquier dirección h de la gravedad. Si la ecuación anterior ha de satisfacerse para cualquier h, la integral entre corchetes debe anularse (la otra opción sería que ese vector entre corchetes fuese paralelo a cualquier dirección h arbitraria, lo que no es posible):
![]()
La última ecuación nos permite calcular explícitamente la posición del centro de gravedad G. Es un punto por el que siempre pasará el eje central de las fuerzas de gravedad, independientemente de la orientación de la gravedad respecto del sólido. Por tanto las fuerzas de gravedad siempre pueden reducirse al peso total pasando por el centro de gravedad.
NOTA: lo anterior quiere decir que puede sustituirse el efecto de la gravedad por una fuerza concentrada a efectos de cálculo del equilibrio. Evidentemente no a otros efectos, como por ejemplo de resistencia del sólido. ¡A nadie nos gustaría que nos tirasen del ombligo (centro de gravedad) hacia abajo con toda la fuerza de nuestro peso!
CENTROS DE VOLUMEN Y DE ÁREA
Adicionalmente, se definen los conceptos de "centro de volumen", y para figuras planas, de "centro de área". Ambos coinciden con el centro de gravedad si el peso específico es constante. Si llamamos C al centro de volumen o de área, su posición viene dada respectivamente por:
![]()
Conviene recordar que los centros de volúmenes y áreas están siempre sobre los elementos de simetría, si existen, ya sean puntos rectas o planos. También será útil recordar que el centro de áreas de un triángulo está a 1/3 de cada una de sus alturas, como indica la figura.

MOMENTOS DE INERCIA
En el estudio de la flexión de barras rectas aparecen las magnitudes de inercia (momentos y productos de inercia) del área de la sección de la barra respecto de una recta. Como ya conoces, su definición es la siguiente:
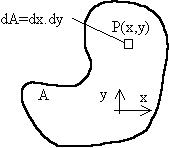

Algunas de las características principales (recordarás la mayoría) de estas magnitudes de inercia son:
- Los momentos de inercia Ix, Iy, son siempre positivos.
- El producto de inercia Ixy puede ser positivo, negativo, o nulo.
- Si el origen de ejes x,y, coincide con el centro de áreas, se llama "centrales" a los momentos de inercia.
- En la resistencia de materiales, prácticamente siempre se usan momentos centrales.
- Existe una orientación de los ejes para la cual el producto de inercia Ixy es nulo: son los ejes principales de inercia.
- De todos los momentos de inercia respecto las
infinitas rectas que pasan por el punto, los principales son el menor y
el mayor.
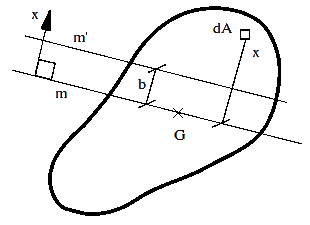
Un resultado de ocasional interés en la asignatura, es el Teorema de Steiner.
Relaciona el momento de inercia respecto de una recta que pasa por el
centro de gravedad, con el momento respecto de otra recta paralela. En
la figura, se toma un eje x, que es perpendicular a las rectas, para
que las
distancias x a la recta que pasa por G tengan signo (esto es, la
distancia b entre las rectas y la distancia x al elemento de área dA):